字符串全排列
用C++写一个函数, 如 Foo(const char *str), 打印出 str 的全排列,
Example 1:
Input: "abc"
Output: "abc, acb, bca, dac, cab, cba"
思路一:非去重递归实现(C语言)
全排列可以看做固定前i位,对第i+1位之后的再进行全排列,比如固定第一位,后面跟着n-1位的全排列。那么解决n-1位元素的全排列就能解决n位元素的全排列了,这样的设计很容易就能用递归实现。
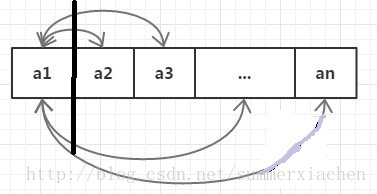
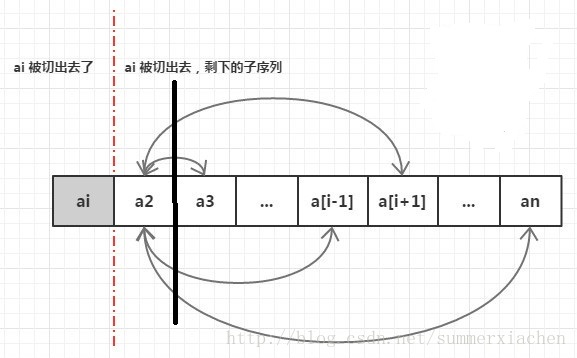
//全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
char t = *a;
*a = *b;
*b = t;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
if (k == m) //当尝试对不存在的数组元素进行递归时,标明所有数已经排列完成,输出
{
static int s_i = 1;
printf(" 第%3d个排列\t%s\n", s_i++, pszStr);
}
else
{
for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
{
Swap(pszStr + k, pszStr + i);
//i是从k开始 i=k;swap(k,i)相当于固定当前位置,再进行下一位的排列
AllRange(pszStr, k + 1, m);
Swap(pszStr + k, pszStr + i);
}
}
}
void Foo(char *pszStr)
{
AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
printf(" 全排列的递归实现\n");
char szTextStr[] = "123";
printf("%s的全排列如下:\n", szTextStr);
Foo(szTextStr);
return 0;
}
###思路二:去重递归实现
由于全排列就是从第一个数字起每个数分别与它后面的数字交换。我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这二个数就不交换了。如122,第一个数与后面交换得212、221。然后122中第二数就不用与第三个数交换了,但对212,它第二个数与第三个数是不相同的,交换之后得到221。与由122中第一个数与第三个数交换所得的221重复了。所以这个方法不行。
换种思维,对122,第一个数1与第二个数2交换得到212,然后考虑第一个数1与第三个数2交换,此时由于第三个数等于第二个数,所以第一个数不再与第三个数交换。再考虑212,它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。
这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。用编程的话描述就是第i个数与第j个数交换时,要求[i,j)中没有与第j个数相等的数。
//去重全排列的递归实现
#include <stdio.h>
#include <string.h>
void Swap(char *a, char *b)
{
char t = *a;
*a = *b;
*b = t;
}
//在pszStr数组中,[nBegin,nEnd)中是否有数字与下标为nEnd的数字相等
bool IsSwap(char *pszStr, int nBegin, int nEnd)
{
for (int i = nBegin; i < nEnd; i++)
if (pszStr[i] == pszStr[nEnd])
return false;
return true;
}
//k表示当前选取到第几个数,m表示共有多少数.
void AllRange(char *pszStr, int k, int m)
{
if (k == m)
{
static int s_i = 1;
printf(" 第%3d个排列\t%s\n", s_i++, pszStr);
}
else
{
for (int i = k; i <= m; i++) //第i个数分别与它后面的数字交换就能得到新的排列
{
if (IsSwap(pszStr, k, i))
{
Swap(pszStr + k, pszStr + i);
AllRange(pszStr, k + 1, m);
Swap(pszStr + k, pszStr + i);
}
}
}
}
void Foo(char *pszStr)
{
AllRange(pszStr, 0, strlen(pszStr) - 1);
}
int main()
{
printf(" 去重全排列的递归实现\n");
char szTextStr[] = "122";
printf("%s的全排列如下:\n", szTextStr);
Foo(szTextStr);
return 0;
}